Binäre Suche
Wir wissen bereits, wie wir in einem Array nach einem bestimmten Element suchen. Hier haben wir die Lineare Suche kennen gelernt, bei der wir ganz stur das Array durchlaufen und immer prüfen, ob wir den gesuchten Wert gefunden haben. Diese Art der Suche ist aber sehr ineffizient und kann sehr lange dauern, wenn das Array groß ist.
Zum Glück gibt es Such-Algorithmen, die wesentlich effizienter und damit schneller zum Ziel kommen. Das entscheidende dabei: Das Array muss sortiert sein! Nicht nur Menschen, sondern auch digitale Geräte finden in einer sortierten Liste das Gesuchte wesentlich schneller, wenn man einen guten Algorithmus hat.
Algorithmus: So funktioniert die Binäre Suche
Die binäre Suche funktioniert im Wesentlichen so: Wir teilen das Array in der Mitte und prüfen dann, ob wir in der linken oder in der rechten Hälfte weitersuchen müssen. Das machen wir dann mit der ausgewählten Hälfte genauso, bis wir den gesuchten Wert gefunden haben oder feststellen, dass der Wert nicht vorhanden ist. Wie wir das Teilen und Suchen genau realisieren, wird im Folgenden beschrieben:
Der Algorithmus
- Setze die Variable indexAnfang auf das erste und die Variable indexEnde auf das letzte Element des Arrays
- Setze die Variable indexMitte auf das mittlere Element des Arrays (hier müssen wir möglicherweise runden!)
- Falls
array[indexMitte]das gesuchte Element ist, können wir die Suche erfolgreich beenden. - Falls
array[indexMitte]> gesuchtes Element => Wir müssen in der linken Hälfte weitersuchen - Falls
array[indexMitte]< gesuchtes Element => Wir müssen in der rechten Hälfte weitersuchen - Falls wir das Element noch nicht gefunden haben: Wiederhole ab dem zweiten Schritt im noch zu durchsuchenden Teil des Arrays.
Beispiel: Wir suchen die Zahl 9
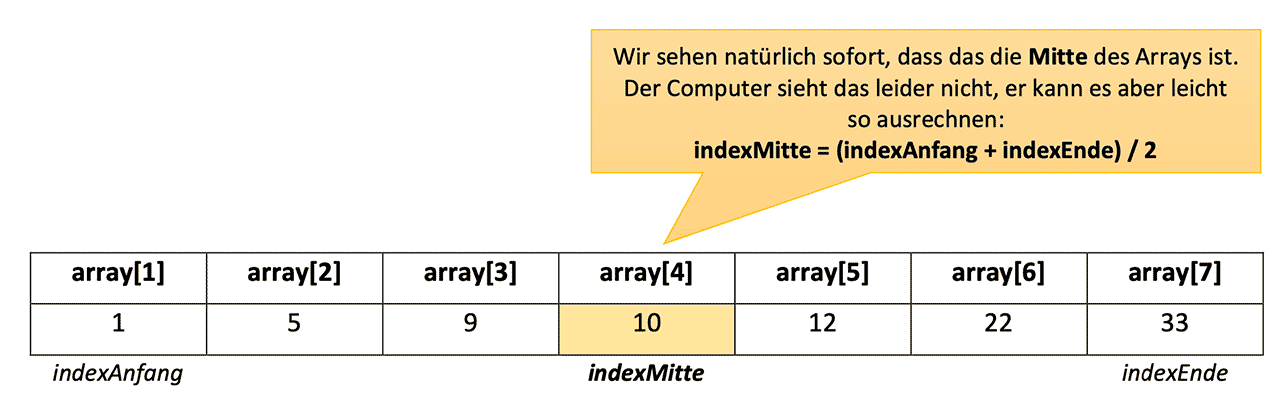
10 > 9 => Wir müssen links suchen!
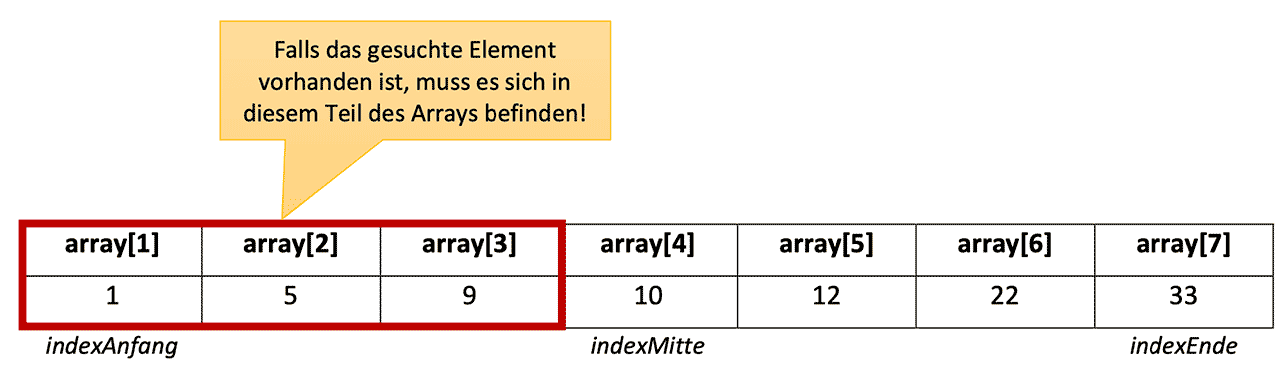
Wir müssen also links suchen! Wie sagen wir jetzt dem Computer, dass er links suchen soll? Ganz einfach: Wir verändern den Wert für indexEnde:
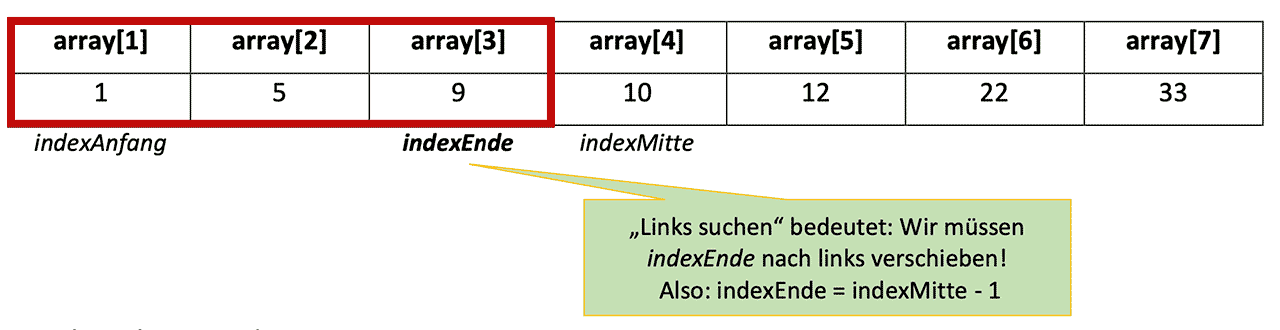
Jetzt berechnen wir die Mitte neu:
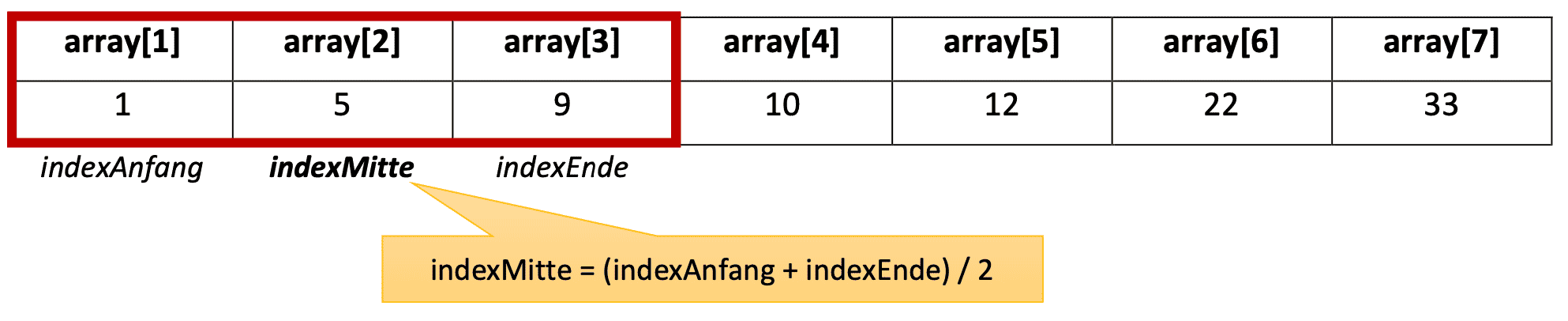
Jetzt geht es wieder von Anfang los: Wir überprüfen, ob wir die Zahl schon gefunden haben oder weiter links bzw. weiter rechts suchen müssen!

5 < 9 => Wir müssen rechts suchen!
Um weiter rechts zu suchen, verändern wir indexAnfang:
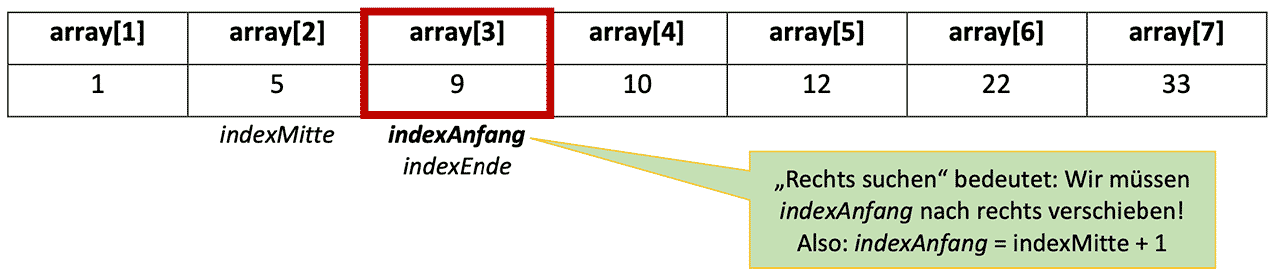
Jetzt berechnen wir die Mitte neu:

array[indexMitte] ist das gesuchte Element! Wir haben es gefunden!
Struktogramm: Ein erster Versuch
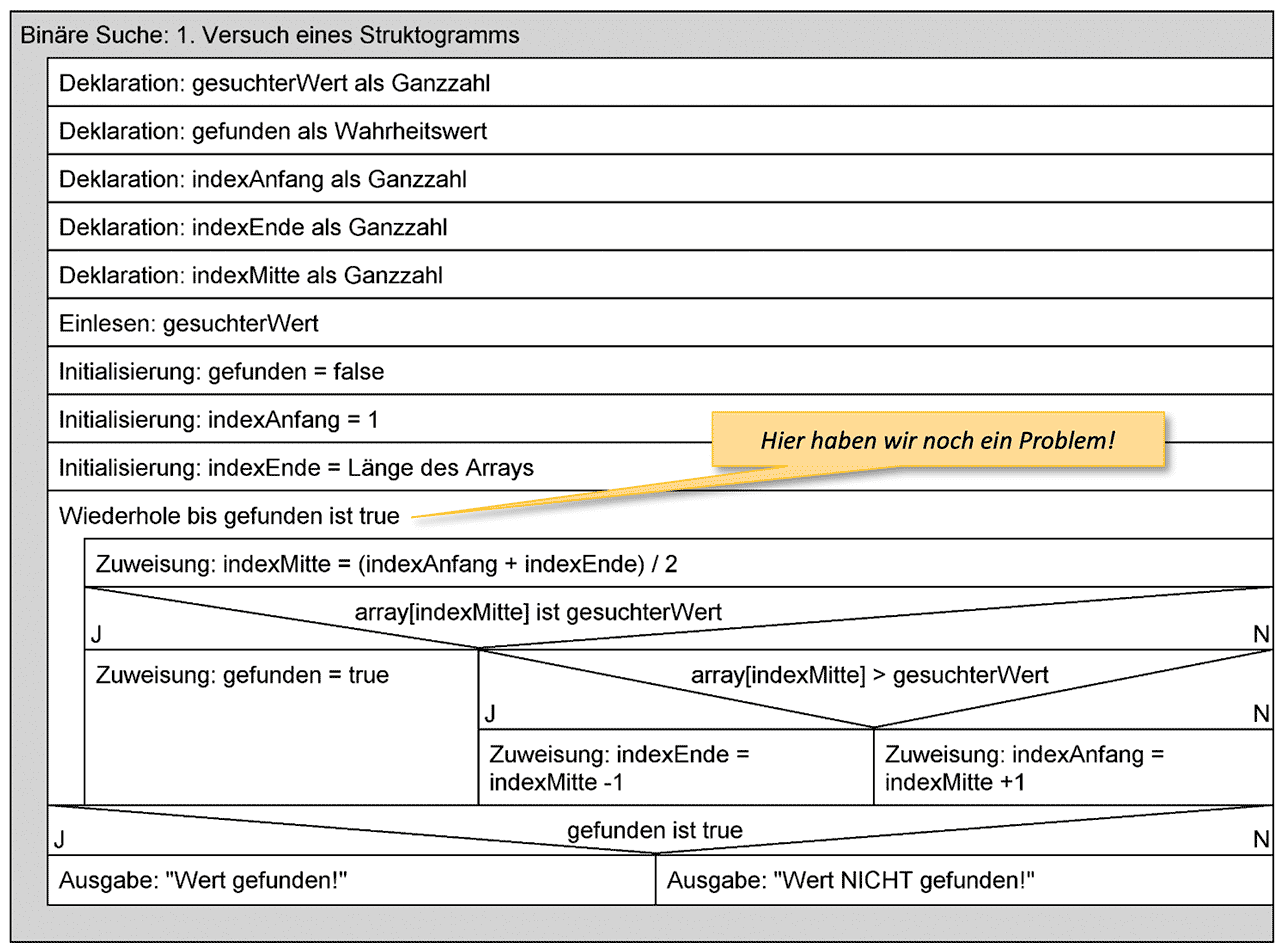
Vereinfachte Version der Binären Suche programmieren
Implementieren Sie das obige Struktogramm im Scratch-Projekt 7500-BinaereSuche-Anfaengeruebung
Beachten Sie, dass das Programm noch nicht in allen Fällen korrekt läuft.
In der Schleife stimmt etwas noch nicht! Wann wird die Schleife denn eigentlich abgebrochen? Klar, dann wenn gefunden den Wert true annimmt, wir das gesuchte Element also gefunden haben.
Was passiert aber, wenn das gesuchte Element gar nicht im Array vorhanden ist? Dann nimmt gefunden ja nie den Wert true an! Wir müssen also eine Möglichkeit finden, es zu erkennen, falls der gesuchte Wert nicht vorhanden ist.
Schauen wir uns dieses an einem Beispiel an:
Beispiel: Wir suchen die Zahl 8!

10 > 8 => Wir müssen links suchen!

5 < 8 => Wir müssen rechts suchen!
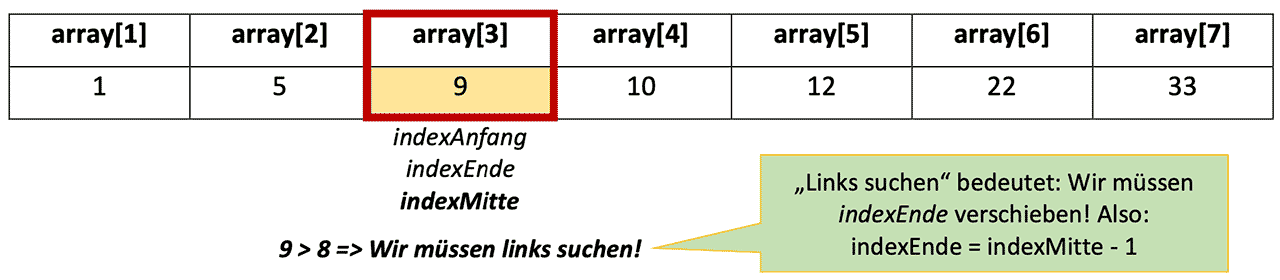
9 > 8 => Wir müssen links suchen!
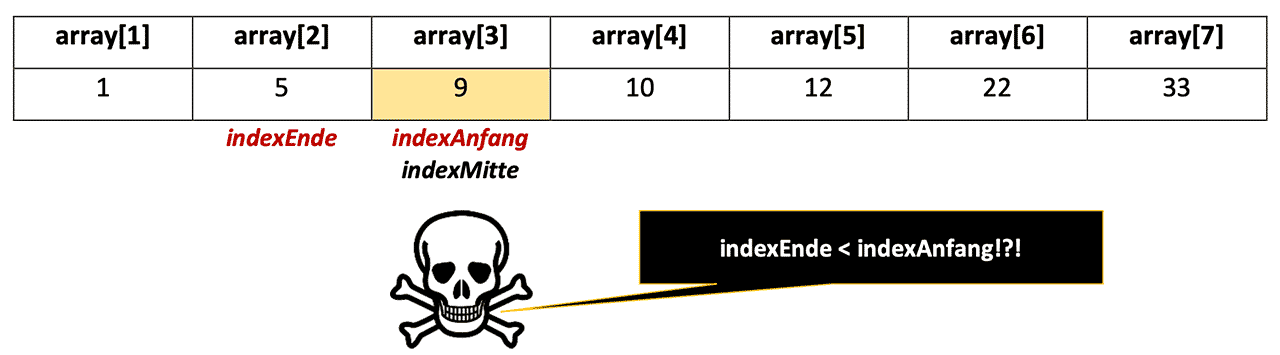
Ist es Ihnen aufgefallen? Das Ende (indexEnde) steht weiter links als der Anfang (indexAnfang) des zu durchsuchenden Bereichs!
Daran können wir erkennen, dass der gesuchte Wert nicht im Array vorhanden ist!
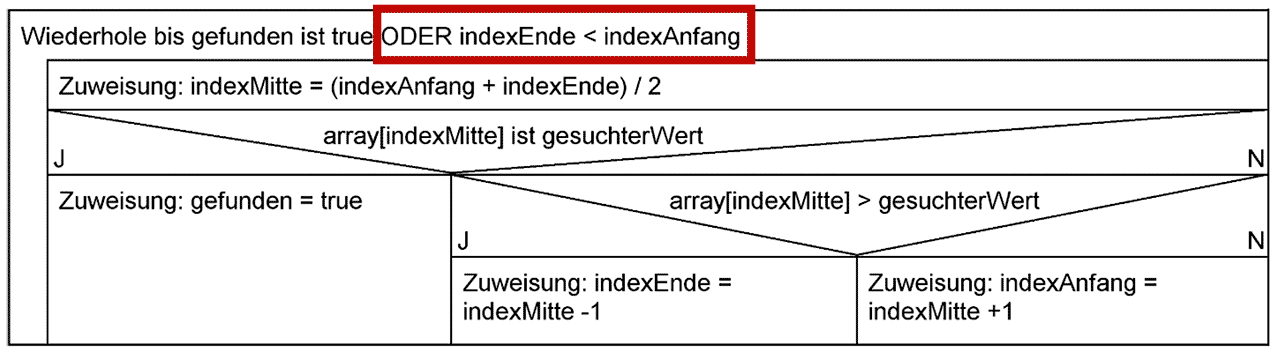
Struktogramm: Zweiter Versuch
Wir ändern die Abbruchbedingung in unserem Struktogramm, so dass die Schleife verlassen wird, sobald wir erkennen, dass wir den gesuchten Wert nicht finden können:
Ein letztes Problem: Runden!
Ein Problem ist uns noch gar nicht aufgefallen: Bei der Berechnung von indexMitte kann es sein, dass wir eine Kommazahl erhalten!
Beispiel:

=> indexMitte = (indexAnfang + indexEnde) / 2 = (1 + 6) / 2 = 3,5
Ein Index muss ganzzahlig sein!
Die Elemente eines Arrays benötigen einen ganzzahligen Index! Das heißt: array[3,5] gibt es nicht!
Das Problem lösen wir ganz einfach: Wenn wir indexMitte mit unserer Formel berechnen, dann runden wir das Ergebnis ganzzahlig!
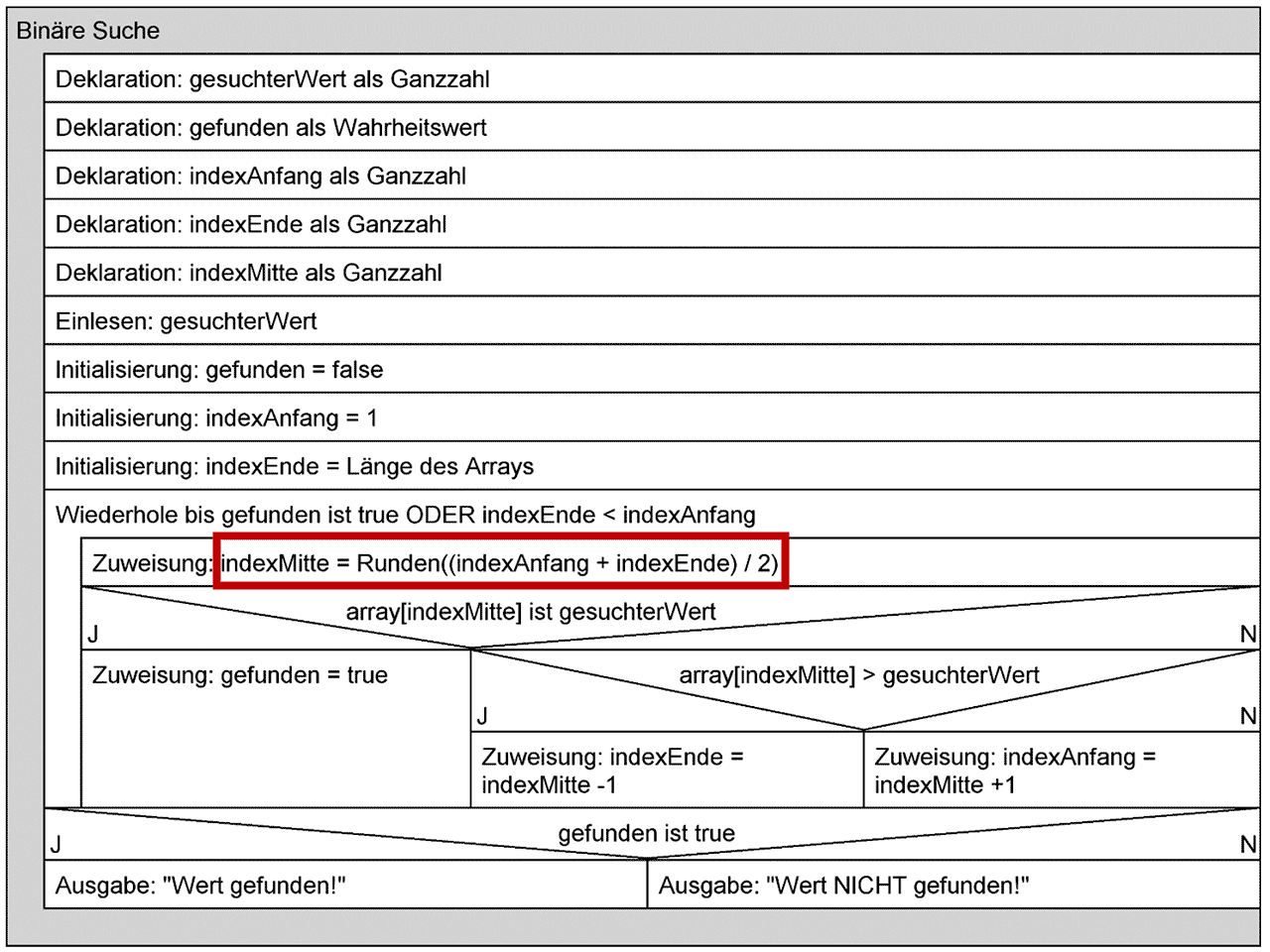
Struktogramm Binäre Suche - Vollständige Version
Wir nehmen die letzten Änderungen an unserem Struktogramm vor:
Aufgaben: Binäre Suche anwenden
(1) Die Zahl 220 suchen
Suchen Sie im folgenden Array nach der Zahl 220. Wenden Sie dabei den Algorithmus Binäre Suche an! Zeigen Sie dabei auch in jeder Zeile, welchen Wert die Variablen indexAnfang, indexEnde und indexMitte annehmen.
Verwenden Sie dafür die Vorlage 7500_BinaereSuche_Aufgaben.docx.
Sie müssen also nichts programmieren, sondern zeigen, wie gesucht wird!
(2) Weitere Aufgaben
Bearbeiten Sie die Aufgaben 2 und 3 aus dem vorhergehenden Arbeitsblatt.
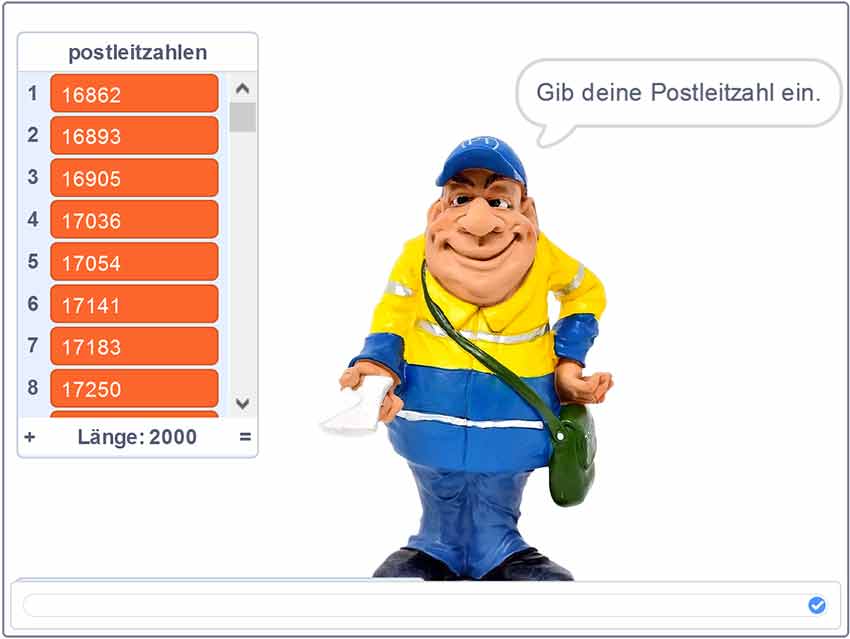
(3) Postleitzahlen suchen
Öffnen Sie in Scratch das Projekt 7500-BinaereSuche-AUFGABE
Entwerfen Sie hier den Programmcode, mit dem Sie im Array nach einer PLZ suchen können!

Erklärvideo: Binäre Suche
Arbeitsblatt: Binäre Suche
Arbeitsblatt »Binäre Suche« (PDF)
Übersicht: Unterrichtsplan Binäre Suche
- Erklärung im Video bis 17:30
- Binäre Suche implementieren in Scratch-Projekt 7500-BinaereSuche-Anfaengeruebung (nach Struktogrammvorgabe Video 17:30 - auch hier als Bild oder siehe unten).
- Besprechen: Welchen Fehler hat dieses Struktogramm? (evtl. hierzu Video 20:10 bis 20:40)
- Auflösung im Video schauen 20:50 bis 22:20 - nachrüsten in Scratch!
- Rundungsproblematik + Implementierung in Scratch: ab 22:20 bis Schluss